This is the second part to the “Your R code probably is 100x slower than it should” blog post. If...
Making NumPy's Standard Deviation 5x faster
The software ecosystem around DATA has grown at an unprecedented rate over the past decade. Libraries in the Python ecosystem such as Pandas and Numpy are now a household name. The popularity and adoption of these libraries make it easy to forget that these libraries were written with the purpose of serving as many people as possible with acceptable performance. In this post we will dive into the performance of one NumPy function, the standard deviation and see how doing a re-implementation of said function can yield great performance improvements.
What are hardware specific optimizations?
Every piece of code you run, runs on hardware. While this is quite obvious it is easy to forget when we deploy to container clusters and serverless functions. These layers of abstraction separate the hardware and the software in such a way that it is a challenge to know what CPU your code is running on.
This is ok. Having these layers of abstraction is useful in many scenarios and may have important cost benefits. However, when working with massive datasets, performance becomes a key factor in determining the cost, the quality and the usability of a data workflow.
Understanding the features of specific hardware can allow us to make the most of it; ChatGPT could not have been possible without deep knowledge of Nvidia GPUs. Of course, you might not be training ChatGPT, but if you have a data process that costs 20 thousand dollars a month, it might be worth it to save 50% or even 75% of the cost.
So, what are hardware specifications optimizations? More than an optimization, it is simply using what the hardware already provides to maximize performance.
Understanding our hardware
In this post we will make use of modern x86_64 CPUs and take advantage of SIMD. SIMD, also known as Single Instruction Multiple Data is a type of parallel processing instructions that allow us to run a single operation over multiple values in a dataset at the same time.
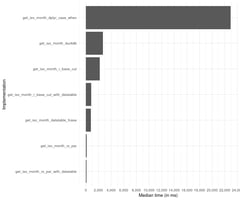
.png?width=1203&height=229&name=Making%20NumPys%20Standard%20Deviation%205x%20faster%20(2).png)
Modern CPUs include many SIMD instructions but we will be trying out AVX-2 (about every CPU from 2013 and beyond should have AVX-2) and AVX-512 (only newer CPUs have this and support is still improving). The example in this post was run on a Zen3 AMD CPU. Once there is greater availability of Zen 5 CPUs on Cloud Solutions we can try newer implementations of AVX-512.
Implementing the standard deviation
Parallelizing the standard deviation may seem tricky, but breaking the problem down may help in understanding how to write effective SIMD code.
The first part of the formula we can parallelize is the mean. The mean requires the sum of values which is a trivial parallelization. We can create four separate sums and sum into every single one at the end we can sum the separate sums into a total sum. The following implementation is in Rust, but the code would be similar in C or C++.
If you are interested in the details behind this code, have a look at the Intel Intrinsics Guide. In essence we are using Rust to get really close to the hardware, by calling the SIMD AVX-2 instruction set directly.
// Sum the elements of the array
let sum = unsafe {
// Take a pointer to the start of the array
let mut ptr = array_view.as_ptr();
// Get a pointer to the end of the array
let end = ptr.add(len);
// Declare the sums
let mut sum_a: __m256d = _mm256_set1_pd(0.0);
let mut sum_b: __m256d = _mm256_set1_pd(0.0);
let mut sum_c: __m256d = _mm256_set1_pd(0.0);
let mut sum_d: __m256d = _mm256_set1_pd(0.0);
while ptr < end {
// Add the values into the sums
sum_a = _mm256_add_pd(sum_a, _mm256_loadu_pd(ptr));
sum_b = _mm256_add_pd(sum_b, _mm256_loadu_pd(ptr.offset(4)));
sum_c = _mm256_add_pd(sum_c, _mm256_loadu_pd(ptr.offset(8)));
sum_d = _mm256_add_pd(sum_d, _mm256_loadu_pd(ptr.offset(12)));
ptr = ptr.offset(16);
}
// Sum the values into a single value and return
sum_a = _mm256_add_pd(sum_a, sum_b);
sum_c = _mm256_add_pd(sum_c, sum_d);
sum_a = _mm256_add_pd(sum_a, sum_c);
sum_a = _mm256_hadd_pd(sum_a, sum_a);
sum_a = _mm256_hadd_pd(sum_a, sum_a);
_mm256_cvtsd_f64(sum_a)
};
We can then parallelize the sum of square differences. We can find the differences in parallel, sum the values in parallel and square the values in parallel.
let square_diff_sum = unsafe {
// Declare the mean as a 4 lane f64
let mean = _mm256_set1_pd(mean);
let mut ptr = array_view.as_ptr();
let end = ptr.add(len);
// Declare the sums and the differences
let mut sum_a: __m256d = _mm256_set1_pd(0.0);
let mut sum_b: __m256d = _mm256_set1_pd(0.0);
let mut sum_c: __m256d = _mm256_set1_pd(0.0);
let mut sum_d: __m256d = _mm256_set1_pd(0.0);
let mut diff_a: __m256d;
let mut diff_b: __m256d;
let mut diff_c: __m256d;
let mut diff_d: __m256d;
while ptr < end {
// 1. Get the diff of 4 values with respect to the mean
// 2. Add the square to the sum
diff_a = _mm256_sub_pd(_mm256_loadu_pd(ptr), mean);
sum_a = _mm256_add_pd(sum_a, _mm256_mul_pd(diff_a, diff_a));
diff_b = _mm256_sub_pd(_mm256_loadu_pd(ptr.offset(4)), mean);
sum_b = _mm256_add_pd(sum_b, _mm256_mul_pd(diff_b, diff_b));
diff_c = _mm256_sub_pd(_mm256_loadu_pd(ptr.offset(8)), mean);
sum_c = _mm256_add_pd(sum_c, _mm256_mul_pd(diff_c, diff_c));
diff_d = _mm256_sub_pd(_mm256_loadu_pd(ptr.offset(12)), mean);
sum_d = _mm256_add_pd(sum_d, _mm256_mul_pd(diff_d, diff_d));
ptr = ptr.offset(16);
}
// Reduce the sums to a single value
sum_a = _mm256_add_pd(sum_a, sum_b);
sum_c = _mm256_add_pd(sum_c, sum_d);
sum_a = _mm256_add_pd(sum_a, sum_c);
sum_a = _mm256_hadd_pd(sum_a, sum_a);
sum_a = _mm256_hadd_pd(sum_a, sum_a);
_mm256_cvtsd_f64(sum_a)
};Now that we have the hardest part down we can divide the sum of squared differences by the length and get the square root. We got the standard deviation down.
(square_diff_sum / len_f64).sqrt()Extending NumPy with our implementation
We just implemented a custom version of the standard deviation that takes advantage of the hardware we will be running on. We just parallelized the standard deviation in a single core. However, we already have a lot of code written in NumPy, it would make no business sense to not take advantage of this code.
Thankfully, PyO3 in Rust allows us to extend NumPy. We can declare a function that takes in a NumPy array and runs our internal function.
#[pyfunction]
fn fast_standard_deviation_avx2(arr: &Bound<'_, PyArray1<f64>>) -> PyResult<f64> {
// Create an ArrayView from the PyArray without copying
let array_view: ArrayView1<f64> = unsafe { arr.as_array() };
Ok(fast_standard_deviation_internal_manual_simd_avx2(
array_view,
))
}
Running the benchmark
After installing our extension we can write a benchmark to test how fast our new implementation is. This is the Python code that benchmarks our functions. You can see that both functions use the numpy array in the same way.
import your_python_is_slow as ypis
import numpy as np
from time import perf_counter
arr = np.arange(2000000000, dtype=np.float64)
N = 5
for _ in range(N):
time_start = perf_counter()
res = np.std(arr)
time_duration = perf_counter() - time_start
print(f'Numpy > took {time_duration:.3f} seconds => {res:.3f}')
for _ in range(N):
time_start = perf_counter()
res = ypis.fast_standard_deviation_avx2(arr)
time_duration = perf_counter() - time_start
print(f'SIMD AVX-2 > took {time_duration:.3f} seconds => {res:.3f}')After we run this we get an impressive 4.7x improvement in performance.
Numpy > took 4.700 seconds => 577350269.190
Numpy > took 4.726 seconds => 577350269.190
Numpy > took 4.734 seconds => 577350269.190
Numpy > took 4.633 seconds => 577350269.190
Numpy > took 4.700 seconds => 577350269.190
SIMD AVX-2 > took 1.100 seconds => 577350269.190
SIMD AVX-2 > took 1.094 seconds => 577350269.190
SIMD AVX-2 > took 1.053 seconds => 577350269.190
SIMD AVX-2 > took 1.106 seconds => 577350269.190
SIMD AVX-2 > took 1.056 seconds => 577350269.190
We can verify the result is the same and that we make a very positive improvement. This can be the difference between hour long data aggregation and just a couple minutes. This is still only AVX-2 which uses 4-lane parallelization on double precision values. Once we have access to newer implementations of AVX-512 (has 8-lane parallelization) we may see a greater improvement without any additional cost in terms of cores or memory.
All of the code for the benchmark can be found on GitHub with a corresponding Dockerfile. Note that this is meant to run on CPUs with at least AVX-2. If you run this on a CPU that does not support AVX-2 or AVX-512 it may not run at all or run at a slow speed. Note that AVX-2 has been available on both AMD and Intel CPU since 2013.
Conclusion
This post was just a sneak peak into what is possible when you write code that is close to the hardware. Having great improvements in data processing speeds is possible with today’s hardware and taking advantage of this can reduce cost and running time of data pipelines that deal with massive datasets or in low-latency environments.
If you want to learn more about how you can improve your data processing pipelines I recommend Your R code is probably 100x slower than it should (Part 2) where we improve the performance of a typical data operation by 100x. If you want specific advice on reducing cloud costs or improving performance let’s have a chat, contact us at hola@ixpantia.com!